Michal,

Matlab's fmincon() provides choice of algorithm: interior point, SQP, trust region.

Interior point algorithms were never designed for accuracy, providing only a few decimal digits precision on easier problems.

SQP is more accurate, disclosed in an excellent textbook by Nocedal & Wright:

https://www.convexoptimization.com/TOOLS/nocedal.pdf

Still, Matlab's SQP implementation would benefit greatly from quadruple precision because it is sensitive to quantization noise of double precision floating point; even on low-dimensional problems.

It is best not to begin with Optimization source code developed at Mathworks.

I speculate that the authors of fmincon() are not specialists in mathematical Optimization. 

It would be better to port original source code developed by mathematicians themselves: Philip Gill, Walter Murray, Michael Saunders, Margaret Wright, Gene Golub, Stephen Wright, Stephen Boyd, Lieven Vandenberghe, Nick Higham, Yinyu Ye, Jan de Leeuw, Henry Wolkowicz, Mar Hershenson, Michael Grant, Jos Sturm, David Donoho, Emmanuel Candes, Monique Laurent, Joakim Jalden, Benjamin Recht, Pablo A. Parrilo, Angelia Nedić.

I know that two of these authors certainly want to see their code translated into Matlab source.

Jon Dattorro

Is an MCT compatible version of Matlab's fmincon() nonlinear optimization available for SQP algorithm?

>>mp.Digits(1)

returns 34.

mp.Digits with argument (.) is a command, not a query.

Why the latency on a command?

A workaround, to avert 2X slowdown in purely double precision programs, is to delete Advanpix from Matlab Path permanently.

Jon Dattorro

To check which BLAS and LAPACK are loaded, 

at Matlab command prompt enter:

version -blas

version -lapack

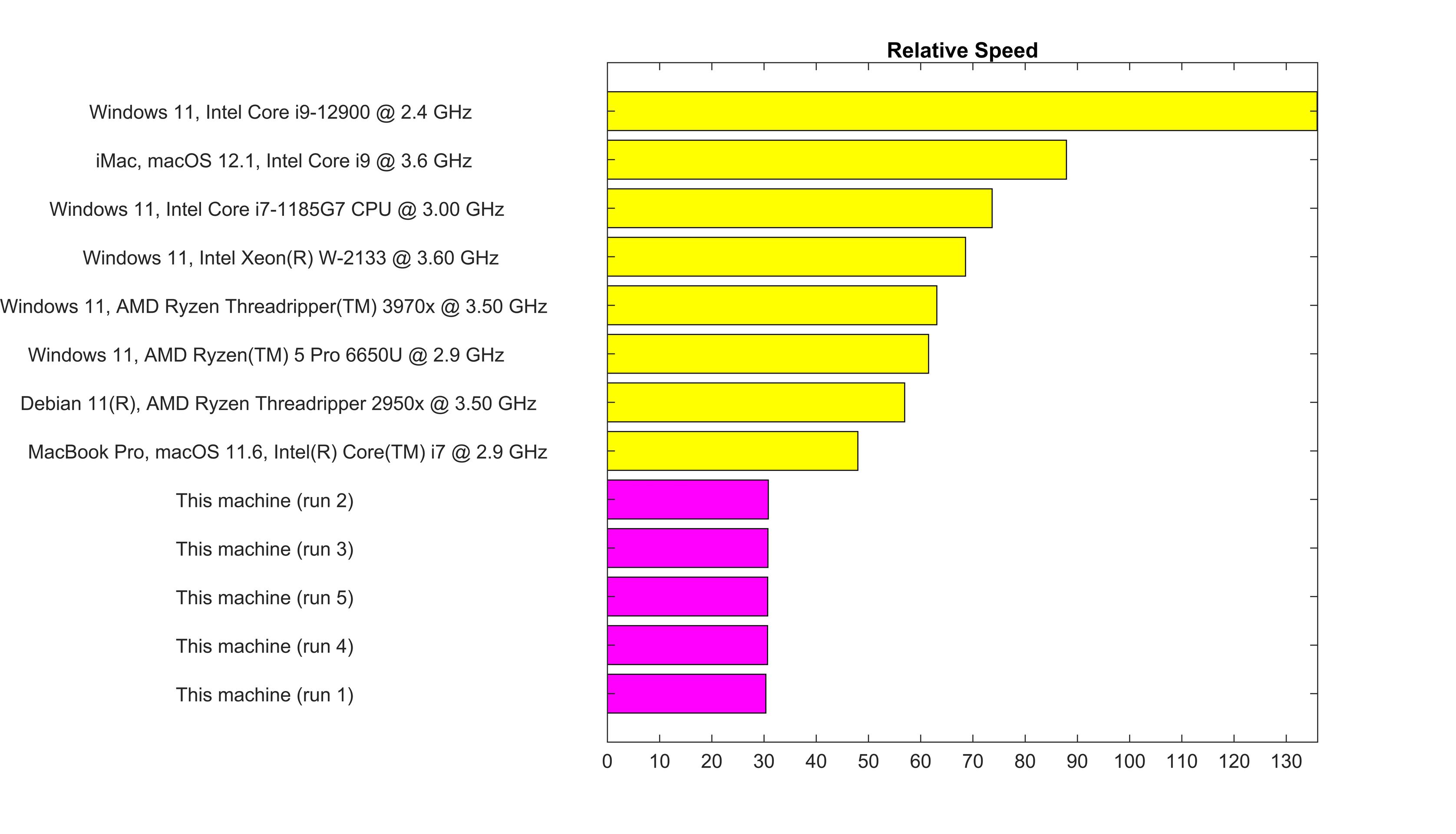
For those who are designing a machine (hardware) specifically to exceed Matlab's bench() function, they need to know that merely having Advanpix in Matlab Path causes 2X slowdown in R2023a.  Solution is to take Advanpix out of Path while building.                    

                                                          ADVANPIX NOT IN MATLAB PATH

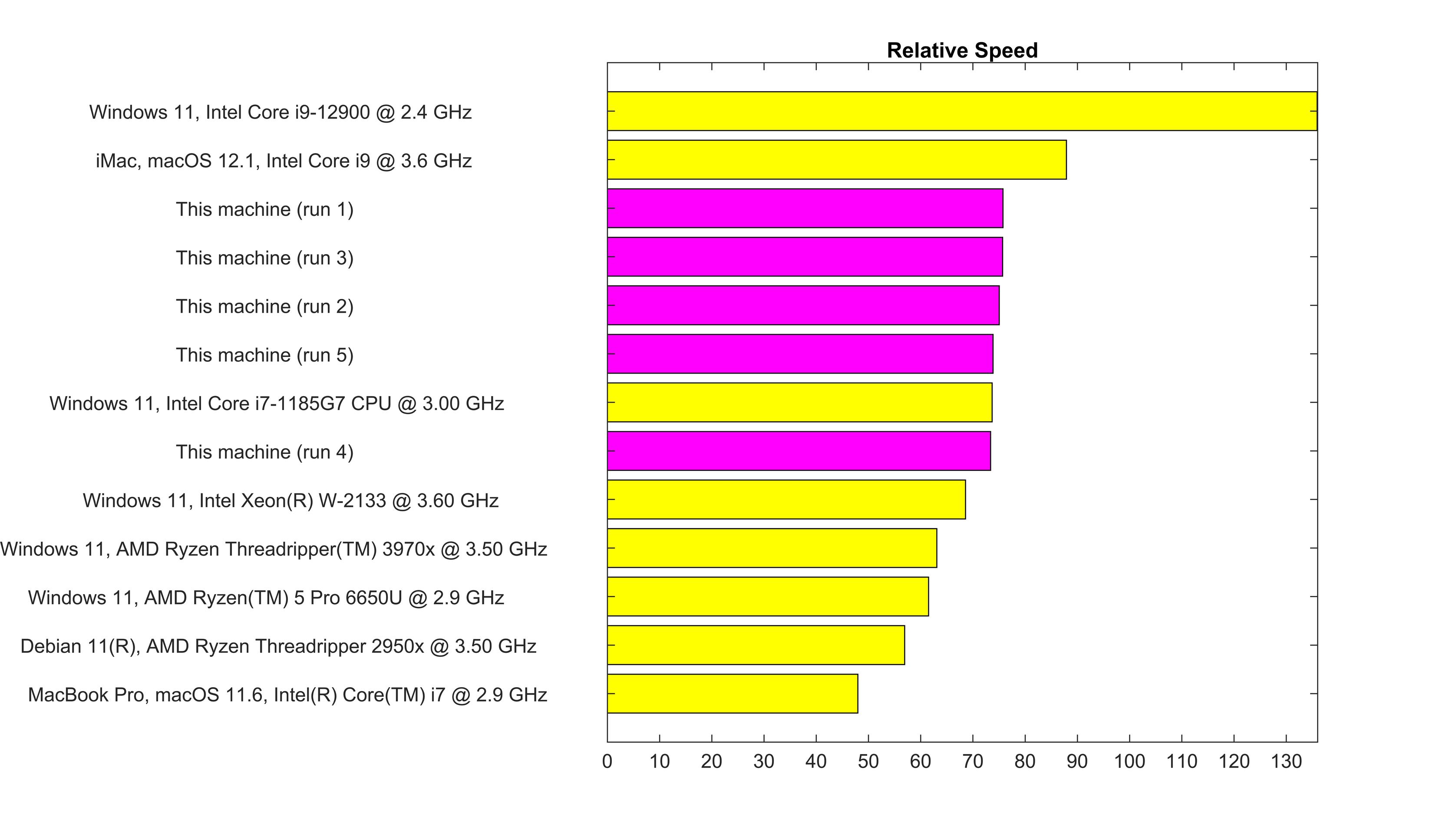
                                                         ADVANPIX IN MATLAB PATH

____________________________________________________________________________

There is a second 2X slowdown caused by using Intel (Matlab R2023a default) BLAS and LAPACK on an AMD CPU.

Solution is to install AOCL from AMD:  amd.com/en/developer/aocl.html

Then, in Windows Environment:
_______________________________________
add to Path:
   C:\Program Files\AMD\AOCL-Windows\amd-blis\lib\ILP64 
add System Variable:
   BLAS_VERSION = AOCL-LibBlis-Win-MT-dll.dll

add to Path:
   C:\Program Files\AMD\AOCL-Windows\amd-libflame\lib\ILP64
add System Variable:
   LAPACK_VERSION = AOCL-LibFLAME-Win-MT-dll.dll

_______________________________________

("I" in front of "LP64" identifies 64-bit OS.)

You will know if you did it right when first time invoking bench() echoes AMD BLAS and LAPACK load.

Jon Dattorro

Yes, true.  But that method is not super quick.  It requires more coding.

Presently, mp.Digits(34) is a special case that instructs MCT to use hardware microinstructions.

Why cannot mp.Digits(16) be similarly reserved to invoke double precision hardware microinstructions?

Presently, mp.Digits(16) is more precise than double precision.  But the same is not true for mp.Digits(34); i.e, had you not invoked hardware microinstructions in that case, then mp.Digits(34) would be more precise than it is now (but slower).

In summary, I think mp.Digits(16) should invoke hardware microinstructions just as mp.Digits(34) does.

We are not suggesting mixed precision.

My original query concerns only passing number-of-digits precision to a subroutine.

User-written subroutines do not respect precision of the arguments; 

i.e, the subroutine defaults to 34 digits regardless of input argument precision.

But consider the example on this page:

>> mp.Digits(100);
>> x = mp.rand(100,100);
>> norm(x-ifft(fft(x)),1)
3.1e-103
 
>> tic; ifft(fft(x)); toc;
Elapsed time is 0.839798 seconds.

The fft() respects input precision of the arguments.
This leads to an expectation of consistency; i.e, a subroutine (user-written or otherwise) should always be executed in precision of the arguments.  But that is not the case. 

Pavel, where is the treatment of subroutine execution precision disclosed in the documentation?  I cannot find it. 

Pavel, on your webpage

https://www.advanpix.com/documentation/version-history/

there is reference to Matlab's nchoosek().

I posted matlab code for linking to its complete (negative argument) binomial coefficient definition here:

https://www.convexoptimization.com/wikimization/index.php/Binomial_coefficient

Here is LaTeX output:

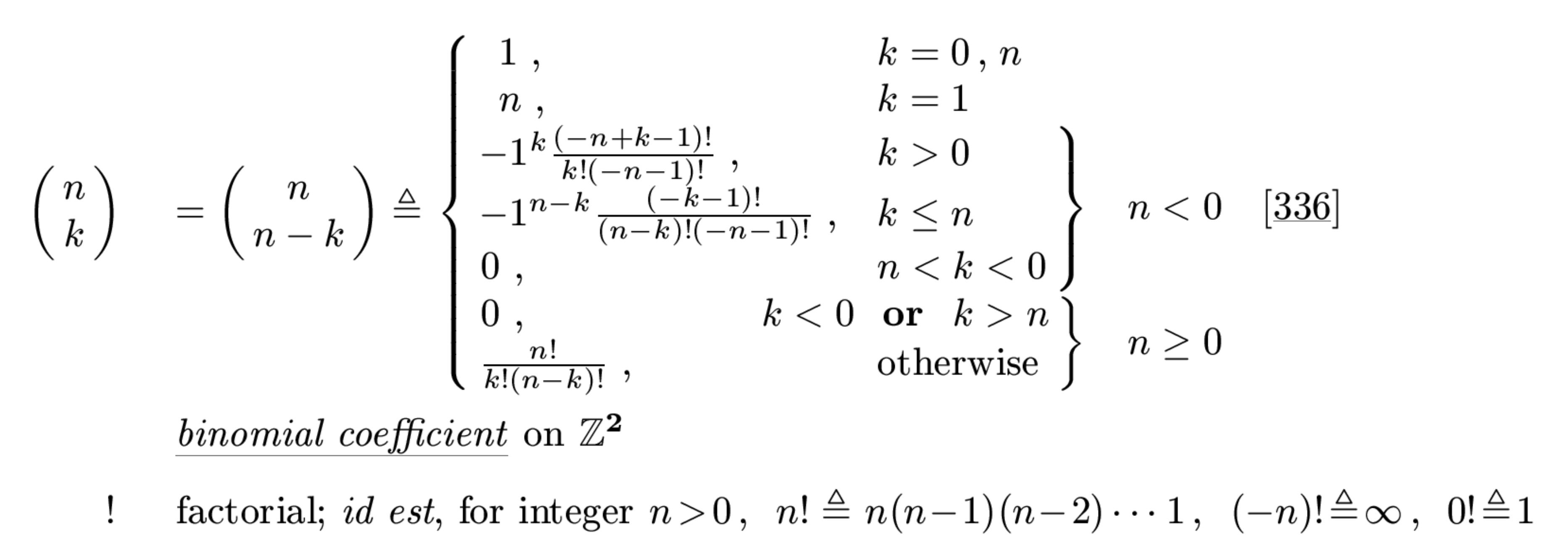
Change .txt to .mat in above; i.e, 

Matlab input:

A = rand(3,3,4,'mp');

mp.write(A, 'mpmatrix.mat');

B = mp.read('mpmatrix.mat');

Matlab output:

Error using mp (line 1331)
Error: uneven number of elements in the rows.
Error in mp.read (line 1017)
A = mp(['[',s,']']);

This .mat file format is read/writable to both Mathematica and Matlab.

Multiprecision Toolbox already understands .mat; e.g, mp.read() and mp.write().

But it coughs on import of multidimensional arrays.  Should it not, if not textual?

This makes communication inelegant, by file transfer with Mathematica.