mp.read mp.write multidimensional matrix
Matlab assumes matrices to be multi-dimensional.
But Multiprecision Toolbox assumes exported matrices are only two-dimensional (can be written on a piece of paper); e.g,
Matlab input:
A = rand(3,3,4,'mp');
mp.write(A, 'mpmatrix.txt');
B = mp.read('mpmatrix.txt');
Matlab output:
Error using mp (line 1331)
Error: uneven number of elements in the rows.
Error in mp.read (line 1017)
A = mp(['[',s,']']);
This cripples communication by file transfer with Mathematica which understands Matlab .mat file format.
@"Change .txt to .mat in above; i.e"
This changes only the extension in file name (txt to mat), but file is still textual.
That is why Mathematica can read it.
Functions mp.write and mp.read were provided solely for the purpose of transferring toolbox's arrays to other software. This can be efficiently done only in textual format. In txt format we store only 2D slices for maximum compatibility with other programs.
The MATLAB's MAT files are of binary format, it is different beast. Toolbox's multiprecision arrays can be stored in binary MAT-files and loaded by toolbox on different OS - using MATLAB's standard commands, save/load.
But Mathematica cannot read it (because there is no support for our toolbox there).
Poor MCT performance on simple arithmetic
I have the following piece of code which takes 100 times longer than simple double precision calculation on my laptop. Is this expected?
s = 0.00001;
delta = 0.9;
e = linspace(0,2,1015);
gamma = 1e-05;
mp.Digits(50);
tic;
for i = 1:100
m = mp((delta/s)^2 - 1); b = mp(-2*(1i*e-gamma)./s);
p1 = m - b.^2/8; p2 = - b*(m + 2)/2;
h1 = (b.^2/4 + m).^2;
h2 = b.^6/32+(3*b.^4*m)/8+(3*b.^2*m^2)/2+27*b.^2*m+27*b.^2+2*m^3;
S = (1/2*(h2+sqrt(h2.^2-4*h1.^3))).^(1/3);
S = 1/2*sqrt(-2/3*p1+1/3*(S+h1./S));
sol = -b./4+S+1/2*sqrt(-4*S.^2-2*p1-p2./S);
sol = double(sol);
end
toc;
P.S. this is the application of Cardano formula to find the roots of a quartic polynomial when coefficients vary.
I have bolded the parts that need to be changed if run using MATLAB double precision arithmetic.
By the way, you need to compute constants (1/3, 2/3) using extended precision: mp('1/3'), mp('2/3').
Otherwise MATLAB evaluates them using double precision. Of course, this must be pre-calculated once before the loop (same as m).
There is still a room for improvement in your code.
amd threadripper
Regarding Advanpix Multiprecision Toolbox, in particular, would there be any disadvantage at all to its operation on an AMD cpu?
Performance comparison
I propose to perform update of the whole MCT performance analysis (paragraph Performance here) with latest versions of MATLAB (2021a_update2), Mathematica (12.3) and Maple (2021.0). I am wiling to perform this analysis, because I have an access to latest version of mentioned SW packages.
I spent some time to discuss with MathWorks guys current "terrible" performance of VPA (Matlab 2021a). So, I thing that is a suitable time to update this comparison and show what is the current performance of MCT together with comparisons.
Sorry to hear about miscommunication with "big boys". But I am not surprised at all, as my experience with them was the same. I communicated with several top technical people, they tried to extract deep technical information about toolbox internals (and why it is so much faster), but never provided anything in return. Later on, I saw they tried to implement some of toolbox's technical "know-hows", but without much success, as I didn't reveal all the details :).
In any case, thank you very much for your time and efforts. Hopefully we can return to this topic later on.
Conversion from string to mp is 4 times as slow than vpa.
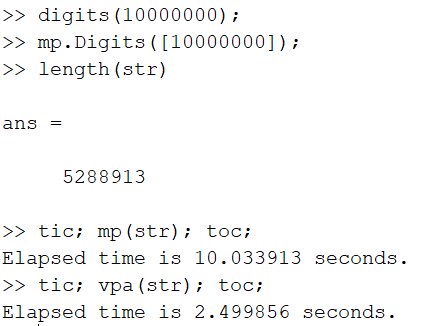
I am trying to speed up a program I wrote using MATLAB's built in VPA function. I am working with integers on the order of 5 to 6 million digits. The bottleneck in my code was converting a string to VPA where the conversion would take around 2.5 seconds. In order to solve this I thought I would use the Multiprecision Computing Toolbox. I downloaded the free trial and only made 2 alterations to my code. I set the mp.Digits value to 10 million (the same as the vpa digits value) and I replaced my vpa() function with mp(). After running the code multiple times I found that the mp version was significantly slower. As you can see in the picture below conversion to mp took 10 seconds while conversion to vpa took 2.5 seconds. Since I am new to the Multiprecision Computing Toolbox I very well could misunderstand how it is supposed to work. If anyone could tell me either a better way to solve my speed issue, and/or why mp is slower then please let me know.
Ok, great, please keep us updated on your experience with toolbox.
nchoosek, binomial coefficient
How do we increase dynamic range of Matlab's binomial coefficient function nchoosek()?
It will not accept multiprecision mp() input.
Jon, I have just released new version of toolbox - 5.3.6.15927.
It doesn't use the MATLAB's implementation of nchoosek anymore.
Instead it is now implemented directly in toolbox core.
>> nchoosek(mp(76), mp(32))
ans =
2695592391875730827550
Please update your environment.
speed up of expm (4.8.3.14440)
The presented improvement of expm speed (version 4.8.3.14440) is for mp.Digits = 34 or 100???
R2020b problem
Matlab R2020b (Windows) is not fully compatible with latest version of MCT:
OMP: Info #273: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
On Linux I can test only old version 4.7.0 Build 13589 which does not report this problem. Just the message:
cat: /etc/upstream-release: Is a directory
on matlab exit.
Yasutaka Hanada benchmark
I just read the Yasutaka Hanada benchmark report which is mentioned at the recent MCT Version history update.
The presented results are really very impressive! Current version of MCT definitely offer best multi-precision performance over commonly used high level computing languages (except MAPLE, which is typically terrible slow). Congratulation!!!
multiplication / addition performance
is there a speed-up when we do the vector-matrix multiplication addition by using your toolbox?
Your question is not clear. "Speed-up" compared to what?
If we would compare it to VPA then we see ~53 times speed-up:
>> A = vpa(rand(1000));
>> x = vpa(rand(1000,1));
>> tic; y = A*x; toc;
Elapsed time is 1.143934 seconds.
>> A = rand(1000,'mp');
>> x = rand(1000,1,'mp');
>> tic; y = A*x; toc;
Elapsed time is 0.021398 seconds.
Customer support service by UserEcho
